数学和计算机的关系，一直是你中有我、我中有你。

计算机程序离不开数学，同时也给数学计算带来便利。

国外知名科普网站Quanta Magazine，对2020年计算机、数学这两门学科的几项重大突破，进行了盘点。

这里面，有困扰了数学家50余年的谜题破解，也有AI与数学结合的身影。

当然，两名数学家疫情隔离期间，破解陶哲轩挑战失败的百年数学问题，也榜上有名。

一起来看看。

TOP1：“量子纠缠”重大突破

今年，计算机领域最重要的突破，是MIP*=RE的证明。

它的证明，意味着利用量子逻辑来计算的量子计算机(而非利用0和1进行计算的经典计算机)，可以从理论上验证大量问题的答案。

来自悉尼科技大学、加州理工学院、德克萨斯大学奥斯汀分校、和多伦多大学的五位计算机科学家，将研究成果联名发表在了一篇叫做《MIP * = RE》的论文上。

这篇论文证明，由经典验证与多个量子理论验证相互作用而确定的语言类别MIP，等同于递归可枚举语言类RE。

也就是说，MIP*=RE多方交互式证明、加上量子纠缠的计算能力，给图灵停机问题提供了一个思路。

对于这篇论文的结论，物理学家在里面看到Tsirelson的物理问题的答案，数学家在里面得到了Connes嵌入猜想的答案。

作者之一的Henry Yuen说道：“如同盲人摸象一样，不同科学领域的人，领略到不同部分，虽然都是正确的，但是都还没搞清楚大象的原貌。”

80年代，计算机科学家发明了交互证明理论和概率可验证明(PCP)，MIP* = RE则是经典的PCP定理，能够在量子纠缠的帮助下递归到无穷。

论文得出结论说，两台机器相互纠缠、相互验证，可以用于解决图灵停机问题。同时，还证明了Connes嵌入猜想是错误的。

他们还引用了经典的两个博弈互证游戏Bell / CHSH，两者无穷无尽的纠缠验证，会提高游戏的胜率。所以最终问题，还是怎么让这个纠缠验证的过程停止的问题。

此外，这篇论文的一作，是悉尼科技大学量子软件与信息中心季铮锋教授。

季铮锋曾于2007年，获得清华大学计算机科学与技术的博士学位。

TOP2：破解“康威扭结”

今年6月，英国著名数学家约翰·康威(John Conway)因患新冠肺炎逝世，留下一个困扰数学界50年的难题“康威扭结”(Conway Knot)。

在他逝世一个月之后，德州大学奥斯汀分校的一位博士小姐姐Lisa Piccirillo，花了一周的时间将其解决了。

多年来，数学家们发现了形形色色的扭结，这些结在拓扑学上可切，但并不是平滑可切。然而，这些扭结的交叉都大于12。

而在交叉点数小于12的扭结中，只有康威结的切片状态一直无法找到。

康威扭结是否平滑可切为何如此重要?

因为平滑可切的扭结，为数学家提供了一条探索四维空间奇特属性的途径。

所以，康威扭结是否为平滑可切，成为了扭结理论重大突破的硬性标准。

Lisa认为，如果可以为康威扭结构造一个相同迹的扭结，那么也许可以更好地与可切不变性配合使用。

于是，她设法构造了一个复杂的扭结，它的迹与康威扭结相同。Lisa使用了一种叫做拉斯穆森S不变量(Rasmussen’s s-invariant)的工具。

结果显示她构造出来的扭结不是平滑可切的，因此推断出，康威扭结也不是平滑可切的。

“这是一个非常美丽的证明。”数学家们纷纷赞叹说。

TOP3：参加IMO的AI

数学已经有了数千年的发展历史，而人类的记忆力有限，即使是一流的数学家，也记不住全部的数学公式和定理。

于是很多数学科学家转向了“数学数字化”，将数千年累积的数学成果，建成一个数字图书馆。

在微软的一个名为Lean的软件程序上，数学家们建立了一个叫做Mathlib的数学基础数据库，这个数据库录入了数学专业大二学生应学到的所有知识。

他们将数学知识汇编成计算机语言，在庞大的数学公式定理库基础上，解决数学难题。

Lean做题的方法跟象棋、围棋AI的算法相同，都是遵循决策树，直到算法找到最优解。

目前，Lean正在筹划参加下一届的IMO(国际奥数竞赛)，比赛结果尚未可知，也有不少人持悲观结果态度。

但是AI做复杂的数学题，是有特别成功案例的。

来自斯坦福大学、卡内基梅隆大学、罗彻斯特理工学院的几位计算机研究者，通过AI的方式，仅用40台电脑、30分钟就解决了困扰数学家90年之久的凯勒猜想。

那么，这一年在数学和计算领域还有什么新的突破呢?

几何学进展 内接方形问题

疫情期间，两位被封闭在家的科学家Andrew Lobb和Joshua Greene觉得百无聊赖。

于是他们动了动手指，解决了一个困扰百年的数学问题，这个数学难题，连陶哲轩都挑战失败了。

这个问题是：任何简单闭合环路，是否总能在其上找到四个点形成一个任意长宽比矩形?

这个问题也叫做内接方形问题，源自1911年。德国数学家Otto Toeplitz预测称，任何简单闭合曲线，都包含四个可以连接形成正方形的点。

这句话听起来很简单，但从古至今，多少数学家费尽脑汁都没有证明出来。

1977年，数学家Herbert Vaughan使用莫比乌斯带解这个内接矩形问题，取得了突破性的进展。

他证明，在三维空间的任何闭合环路中，都至少存在这样四个点，能够构成一个矩形。

天才数学家陶哲轩，使用积分方法，解决了特定情况下的内接方形问题。

他用积分方法证明，在曲线由两个常数小于 1 的 Lipschitz 图形组成的这种特殊情况下，该曲线一定存在四个能组成正方形的点。

但是两者都未证明：是否任意长宽比的矩形(包括正方形)都能存在。

在Andrew Lobb和Joshua Greene的方法中，他们将莫比乌斯带嵌入四维辛空间中，证明了莫比乌斯带可以嵌入到四维辛空间中而不相交。

这意味着每一个封闭的光滑曲线必须包含四个点的集合，这四个点可以连接在一起形成所有长宽比的矩形。

十二面体的新发现

数学家花了2000多年的时间，来研究正四、六、八、十二、二十面体，这些特殊形状也叫做柏拉图多面体。多年来，数学家仍对对它们知之甚少。

关于柏拉图多面体一直有个思考，假设从柏拉图立体的一个角出发，是否存在一条直线路径，不用经过其他角，就可以回到原来的角?

对于等边三角形或者正方形组成的四面体、立方体、八面体、二十面体，科学家得出的具体结论是：不存在。必须经过其他角，否则永远回不到出发点。

然而正十二面体是由五边形组成，是否也符合这个定理?

Jayadev Athreya，David Aulicino和Patrick Hooper在《实验数学》杂志上发表了关于十二面体的研究。

他们认为，由于正十二面体由五边形组成，五边形和正十二面体又有几何上的联系，前者的高度对称性可以用于阐明后者的结构。

因此，研究者能够识别十二面体回到出发点所有直线路径，并根据十二面体的隐藏对称性对这些路径进行分类。

正十二面体存在无数条这样的直线路径，这些路径还可以划分为31个自然族。

数学思想的升华 升级Langlands数学桥

17世纪法国数学家提出了“费马最后的定理”。断言，当整数n>2时，关于x，y，z的方程x2+y2=z2没有正整数解。

1995年，它被英国数学家安德鲁·威尔斯(Andrew Wiles)证明，经历了300多年。

威尔斯同时提出了数学桥的概念。意思是，这个等式就是两个数学领域之间的桥梁，连接好这座桥，就解开了这个不定式。

然而这只是Langlands项目的一小部分。Langlands项目由加拿大数学家罗伯特·兰兰兹(Robert Langlands)提出，旨在研究数论与几何之间联系的网络猜想，被看作是现代数学研究的最大项目。

数学家们将这个方法扩展到有理数系数和椭圆曲线之间的联系。最近，还覆盖到了简单的无理数系数。但是涉及到了虚数，或者更高的指数，例如4或5，他们方法也不奏效了。

于是，芝加哥大学的Frank Calegari和Facebook的科学家David Geraghty为了克服上述障碍，在网上发布论文，是关于怎么建立一个更加通用的不定式的桥梁，并提出了三个猜想。

为了证实这三个猜想，数学家们迅速举办了一个秘密的研讨会，整理成了有10个人署名的论文。

虽然这篇论文的研究成果在数学领域的Langlands项目中取得了巨大的突破，但是对于指数大于6，或者2个变量以上的不定式，仍旧没有解决办法。

所以，Langlands项目还有拓展空间。

多项式与幂级数

物理学中的排斥力，在数学中也存在。

多伦多大学的 Vesselin Dimitrov，就证明了它们的存在，并且获得了实验结果。

一般情况下，多项式的根数与其次数值一样多。所以X2 - 4具有两个根，而X 5 - 7 X 3 + 2 X 2 - 4 X - 9有五个根。

数学家很想知道多项式的根与根之间有什么联系。

这里引入一个分圆多项式，所谓的分圆多项式就是不可约的多项式，数学家发现其根遵循特定的几何方式，根都分布在一个圆内，取名叫做“团结之根”。

但是实际上，大多数都是非分圆多项式。

数学家预测，每个非分圆多项式必定有一个根在圆外。

他们猜想这个是由于“排斥力”，就像物理中的电子一样，它们最小的根落在圆内，像磁铁一样拥有排斥力，将其他根排斥到圆外。

但是长期以来，数学家们没能证明这个理论。

Dimitrov做到了，他将多项式的根的大小的问题转换成幂级数。幂级数就像多项式，有无限个解。

他从一个非分圆多项式入手，找到它的根，并把这些根取不同的幂，再将它们相乘，然后取这个积的平方根。最后，根据这个平方根，构建出一个具有多项式本质属性的幂级数。

Dimitrov证明了幂级数的系数必然是整数，如果它的Hankel determinants也很大，那么，非分圆多项式的一个初始根必然也很大。于是，就证明了多项式的根与幂级数之间的联系。

其他数学家评论说：“他的方法很精妙，间接证明了关于排斥力的猜想。”

来自牛津大学的青年数学家詹姆斯·梅纳德(James Maynard)攻下了困扰大家80年的数学难题——Duffin-Schaeffer猜想。

Duffin-Shaeffer猜想是度量丢番图逼近中的一个重要猜想，由物理学家Richard Duffin和数学家Albert Schaeffer在1941年提出。

众所周知，大部分的实数都是π、√2这样的无理数，它们是无法用分数来表示的。

这个猜想假设 f：N→R≥0是具有正值的实值函数，只有当级数：

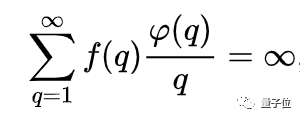
是发散的(q>0，φ(q)为欧拉函数，表示比q小且与q互质的正整数的个数)，对于无理数 α 而言，就存在无穷多个有理数，满足不等式 | α-(p/q) |< f(q)/q。

这个证明过程困扰数学家数年，James Maynard和蒙特利尔大学的Dimitris Koukoulopoulos将它攻破了。

在他们的证明中，他们用分母创建了一个图：把分母绘制成图上的点，如果两个点有许多共同的质因数，就用线将两点连接起来。

这样一来，图的结构就编码了每个分母所近似的无理数之间的重叠。原本这种重合度是难以直接测定的。

由此，他们证明了Duffin-Schaeffer猜想的正确性。

以上就是Quanta Magazine评选出来的，今年计算机-数学领域最重要的几项研究进展。

你认为这里面，哪些研究更有学术价值?

又或者说，是否还有没上榜单的，但同样是今年重大的研究突破?

关键词： 奥数AI